mikeash.com: just this guy, you know?

next up previous contents
Next: Accès mémoire Up: Optimisation de lancer de Previous: Optimisation de lancer de   Contents

Calcul des adresses

On a vu dans la partie 5.1 qu'il faut minimiser les conversions entre les valeurs int et float pour avoir la plus grande vitesse. La boucle principale de lancer de rayons fait parcourir un rayon dans les données volumiques. À partir de la taille du cube, les points d'entrée et de sortie, et les paramètres de LOD, on calcule un $dx$, $dy$, et $dz$, et un nombre d'échantillons à prendre. On commence avec le point d'entrée et on ajoute les deltas à chaque étape jusqu'à la réalisation de toutes les étapes ou jusqu'à la couleur maximale. Alors toutes ces coordonnées ne peuvent pas être des entiers, car on a souvent des deltas qui sont entre $0$ et $1$. On doit alors faire trois conversions float-int à chaque étape de cette boucle.

Figure: Une étape de la boucle intérieure de lancer de rayons.

Hormis ces conversions, il faut ajouter le calcul de l'adresse du voxel courant à partir de ses coordonnées.


\begin{displaymath} adresse = x_i + y_i \times size_x + z_i \times size_x \times size_y \end{displaymath}

Les multiplications dans ce calcul sont coûteuses. Il faut aussi borner les coordonnées pour éviter des problèmes d'arrondis, ce qui demande des comparaisons coûteuses.

Lorsque le cube est de taille $2^n \times 2^n \times 2^n$ il est plus facile de convertir une position dans le cube en une adresse en mémoire. Chaque dimension utilise un nombre entier de bits dans l'adresse. Par exemple, pour un cube de $32 \times 32 \times 32$, chaque coordonnée prend exactement 5 bits dans l'adresse du voxel.


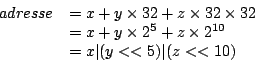
\begin{displaymath} \begin{array}{rl} adresse & = x + y \times 32 + z \times 3... ...s 2^{10} \\ & = x \vert (y << 5) \vert (z << 10) \end{array}\end{displaymath}

Ce calcul n'utilise que les opérations bitwise de C, qui sont normalement très rapides (Voir Figure 13 pour une représentation graphique de l'adresse pour le cube de 32x32x32).

Figure: L'organisation des coordonnées dans l'adresse d'une valeur dans un cube de 32x32x32.

Pour éviter les conversions float-int, on utilise une représentation en virgule-fixe. Notre implantation utilise une mantisse de 20 bits et alors un exposant fixé à $2^{-20}$. Cette représentation permet une conversion en un entier pour les opérations peu coûteuses. [19]

On peut combiner ces deux opérations. Pour chaque coordonnée on a successivement un shift à droite pour changer en entier, et un shift à gauche pour le calcul de l'adresse. Ces deux opérations peuvent être simplifiées grâce à un masque de la manière suivante : 

// 1
y_int = y >> 20
y_int = y_int % ysize
adresse = adresse | (y << log2(xsize))

// 2
xshift = log2(xsize)
yimask = (y - 1) << xshift
yishift = 20 - xshift

// 3
adresse = adresse | ((y >> yishift) & yimask)

Le calcul dans 1 est remplacé par le calcul dans 2, qui est fait une seule fois, et le calcul dans 3 qui est fait à chaque calcul d'adresse.

Le nombre d'opérations est le même, mais cette version ajoute une fonctionnalité, elle borne les valeurs qui deviennent trop grandes. Alors, en deux opérations par coordonnée et deux opérations en plus pour combiner les résultats, on peut faire tout le calcul de l'adresse d'une valeur : 

offset = ((sx >> xishift) & ximask) |
         ((sy >> yishift) & yimask) |
         ((sz >> zishift) & zimask);

next up previous contents
Next: Accès mémoire Up: Optimisation de lancer de Previous: Optimisation de lancer de   Contents
Michael Ash 2005-09-21

Code syntax highlighting thanks to Pygments.
Hosted at DigitalOcean.